ОСНОВИ ДИСКРЕТНОГО АНАЛІЗУ.
Автори: Н.Д.Федоренко,В.В.Демченко

     3.11. МЕТОД КАРНАУ-ВЕЙЧА

      Якщо число змінних логічної функції мале () , знаходження мінімальних форм можна проводити за допомогою спеціальних таблиць, які називають діаграмами Вейча або картами Карнау. Нехай n=4 , тобто 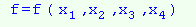. Карта Карнау для чотирьох змінних являє собою квадрат, що розбитий на 16 малих квадратів (4х4). Складемо карту Карнау.

Для змінних 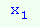та відведемо вертикальну сторону карти, а для - горизонтальну (порядок необов'язковий).

За таких умов карта Карнау приймає вид (таблиця 13).

Зміст карти в тому, що функція задається таблицею, але не в стовпчик, як завжди, а на площині у вигляді 16 квадратів. Набори змінних використовуються в порядку так званого коду Грея (0;0); (0;1); (1;1); (1;0). На карті Карнау сусідні набори відмінні лише однією координатою від сусіднього по розміщенню. Значення функції записують в малих квадратах. По таблиці Карнау з'ясовують, які квадрати карти Карнау можна закріпити тією чи іншою імплікантою якщо два сусідніх рядки чи два сусідніх стовпчика заповнені одиницями, то їх можна покрити однотермовим імплікантою, тобто, якби в перших двох рядках всюди були одиниці, то:

.

Таблиця 13

.

Зауважимо, що карту Карнау слід уявляти так, що вона намальована не на площині, а на поверхні, що має форму тору, в якому сусідніми будуть перший та останній рядки, перший та останній стовпчики. Тобто, можна стверджувати, що однобуквеним імплікантам відповідають або два сусідні рядки або два сусідніх стовпчики.

Двотермові імпліканти і т.д. розглядають так: імпліканті відповідає третій рядок. Якщо цей рядок покрито одиницями, то всі вони покриваються імплікантою . Аналогічно знаходяться трьохтермові, чотирьох-термові імпліканти. Тобто, за допомогою карти Карнау графічно виконуються операції склеювання, поглинання, об'єднання одиниць та груп одиниць одні з одними. Продемонструємо метод Карнау на прикладі.

      Приклад 7. Нехай функція задано таблицею 14.

Таблиця 14

.

Розв'язання. Проаналізуємо задану таблицю істинності і позначимо квадрати, що вміщують одиниці буквами.

По таблиці видно, що однотермові імпліканти відсутні, бо не має двох сусідніх стовпчиків чи рядків, які вміщують лише одиниці.

Будемо шукати двотермові імпліканти, тобто чотири квадрати з одиницею, що витягнуті в одну лінію або складені у великий квадрат. Бачимо, що перший рядок (квадрати ) - утворює лінію, яка покривається та , отже отримано імпліканту .

Квадрат , що складається з одиниць, повністю покривається імплікантою .

Квадрат покривається імплікантою (квадрат отримано замкненням карти до утворення тору). Більше квадратів утворити не можна, тобто

.

В таблиці непокритими залишилися дві одиниці (квадрати i та j). Покрити їх неможливо, тобто необхідно витратити на них трьохтермову імпліканту .

Всі одиниці покриті імплікантами, за методом Карнау-Вейча мінімальна нормальна форма функції має вид:

.

Отриманий результат можна перевірити по таблиці істинності і впевнитися, що МНФ функції f дає всі значення вихідної функції. Зауважимо, що зовнішня загальна простота методу, повертається складною програмою при реалізації алгоритму Карнау-Вейча на комп'ютері.

ЗМІСТ