ОСНОВИ ДИСКРЕТНОГО АНАЛІЗУ.
Автори: Н.Д.Федоренко,В.В.Демченко

     ГЛАВА 1. КОМБІНАТОРНІ СХЕМИ

     ВСТУП

      Комбінаторику в деякому змісті можна розуміти як синонім терміну "дискретна математика" - дослідження дискретних скінчених математичних структур.
Для подальшого розглядання комбінаторних схем, нагадаємо деякі з понять теорії множин.
- елемент належить множині ,
- елемент не належить множині ;
- потужність множини (кількість її елементів).
- об'єднання двох множин;
- перетин двох множин;
- різниця двох множин;
- прямий декартовий добуток двох множин;
- порожня множина;
- універсальна множина, або універсум;
- доповнення до множини ;
- неперетинні множини.
Якщота- скінчені множини, причому, то можна сформулювати правила суми та прямого добутку.
Нехай , то
- правило суми.

      Інтерпретація. Якщо елементможна вибратиспособами із множини, а елемент-способами із множини, то елемент можна вибрати- способами.
Правило суми можна розширити і на множин, тобто. якщо,, то .
Нехайіскінчені множини,, тоді- правило прямого добутку.

      Інтерпретація. Якщо елементможна вибратиспособами, елемент- способами, то вибір парив указаному порядку можна виконати



способами.
Причому, вибір елементів множинине залежить від способу вибору елементів множини. Якщо,- довільні множини, , то
.

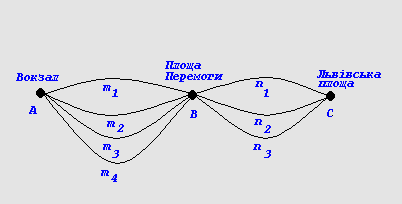
      Приклад 1. З залізничного вокзалу м. Києва до Львівської площі ведуть чотири дороги, які проходять через площу Перемоги, від якої існує три дороги до Львівської площі. Скількома шляхами можна попасти з вокзалу до Львівської площі?
Розв'язання. Побудуємо схему вокзал (рис.1)

Рис.1
Введемо дві множини - дороги ізв. Шлях ізв, це параде.
- множина всіх можливих пар, тобто доріг ізв, загальна їх кількість. Отже, з вокзалу до Львівської площі можна пройти 12 шляхами.

ЗМІСТ